특정 노드에서 다른 노드로 가는 최단 경로를 알려주는 알고리즘
음의 간선이 없을 때 사용
단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 그리고 해당 노드를 거쳐 가는 경로를 확인하며, 최단 거리 테이블을 갱신하는 방식으로 동작한다.
우선순위 큐 라이브러리는 (가치,물건)으로 구성된다면, 첫 번째 원소(가치)를 기준으로 우선순위를 설정한다.
# 한 지점에서 다른 특정 지점까지의 최단 경로를 구해야 하는 경우
#노드와 간선의 개수가 많을 경우 유리
#우선순위 큐 라이브러리 > 최소 힙 구조 사용- 값이 낮은 데이터를 먼저 삭제
#튜플 데이터를 (거리,노드)로 큐에 삽입
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)
n,m = map(int,input().split())#노드, 간선 개수 입력
start = int(input()) # 시작노드
# 각노드에 연결되어있는 노드에 대한 정보를 담는 리스트
graph = [[] for i in range (n+1)]
distance = [INF] * (n+1)
# 모든 간선 정보 입력
for _ in range(m):
a,b,c = map(int,input().split())
# a번 노드에서 b번 노드로 가는 비용이 c
graph[a].append(b,c)
def dijkstra (start):
q=[]
heapq.heappush(q,(0,start))
distance[start] = 0
while q: #큐가 비어있지 않다면
dist,now = heapq.heappop(q) #가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
# 처리된 적 있는 노드라면 무시
if distance[now] < dist :
continue
#현재 노드와 인접한 다른 노드들 확인
for i in graph[now]:
cost = dist +i[1] #i[1] => c
#현재 노드를 거쳐 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance [i[0]] = cost
heapq.heappush(q,(cost,i[0])) #(가치,노드)순으로 삽입
dijkstra(start)
#모든 노드로 가기 위한 최단 거리를 출력
for i in range(1,n+1):
if distance[i] == INF:
print('infinity')
else:
print (distance[i])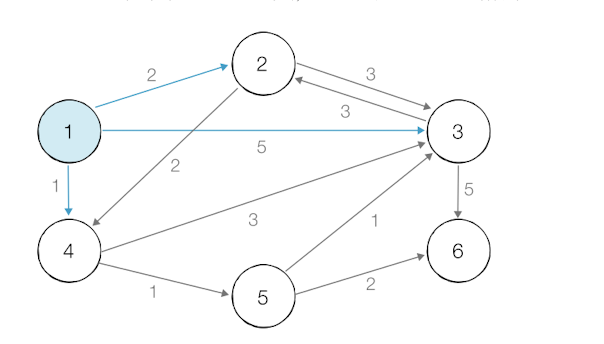

1에서 갈 수 있는 2,3,4 거리 업데이트
그 중 최단거리인 4번 노드 선택
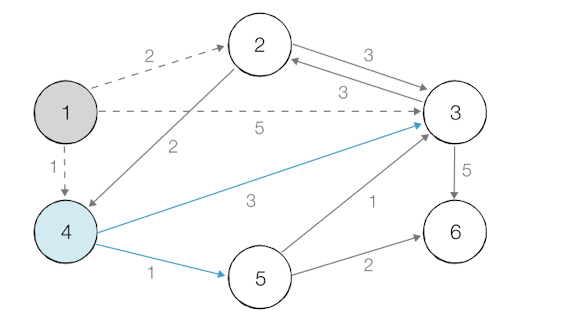
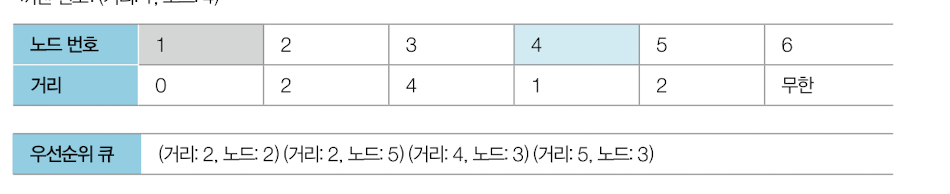
4번 노드에서 갈 수 있는 3,5 노드의 거리 업데이트
최단거리 5번 노드 선택
전 과정을 큐가 빌 때 까지 반복!
'[Algorithm]' 카테고리의 다른 글
| 완전탐색 - 최대최소차 (0) | 2023.05.08 |
|---|---|
| 완전탐색 - 여러 구간, 구간 합의 최댓값이 최소가 되도록 (0) | 2023.05.08 |
| [백준] - 2839 설탕배달 (0) | 2022.05.27 |
| [백준] 9251-LCS (0) | 2022.05.25 |
| 백준 11792- [재귀함수] 하노이 탑 이동순서 (0) | 2021.09.28 |
![[이코테] 다익스트라 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F99vDI%2FbtrDJvoN99k%2FAAAAAAAAAAAAAAAAAAAAALc1NvmUV6pFvMnHGIWaS0qwvHCmYUayLqY8zXoRmwkw%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3Dooi4QKMyid4ziTrXQR%252BwsXmquNI%253D)